Généralité sur les systèmes de numération
Objectif :
- Définir les termes numération, système de numération, Base
- Lister les bases usuelles (2 - 8 - 10 - 16)
Nous avons pris l'habitude de représenter les nombres en utilisant dix symboles différents : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ce système est appelé système décimal (ceci signifie dix).
I- Système de numération
La numération désigne les techniques de représentation des nombres. Aussi elle concerne les mots, les signes ou les symboles qui ont permis aux différents peuples d'énoncer, de mimer ou d'écrire ces nombres. Par définition la numération permet de représenter un nombre par la juxtaposition ordonnée des symboles pris dans un ensemble.
Un système de numération décrit la façon avec laquelle les nombres sont représentés.
Un système de numération est décrit par :
- Un alphabet A : ensemble de symboles ou de chiffres.
- Des règles d'écritures des nombres : juxtapositions de symboles.
Exemple de système de numération
Numération décimale : C'est le système de numération le plus pratiqué actuellement. L'alphabet est composé de dix chiffres : A= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
- Le nombre 10 est la base de cette numération
- C'est un système positionnel. Chaque position possède un poids.
Par exemple, le nombre 4134 (4 représente le chiffre des millième, 1 le chiffre des centaines, 3 le chiffre des dizaines et 4 le chiffre des unités) s'écrit comme : 4*103 + 1*102 + 3*101 + 4*100.
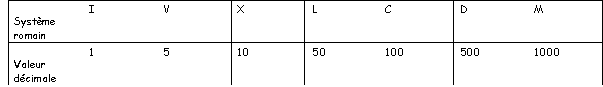
- Lorsqu'un symbole est placé à droite d'un symbole plus fort que lui, sa valeur s'ajoute : CCLXXI→271 (100+100+50+10+10+1)
- Lorsqu'un symbole est placé à gauche d'un symbole plus fort que lui, on retranche sa valeur : CCXLIII→243 (100+100+40+3)
- On ne place jamais 4 symboles identique à la suite : 9 s'écrit IX et non VIII
- La plus grand nombre exprimable est : 3999 (MMMCMXCIX)
- Système inadapté au calcul.
I- NOTION DE BASE
Le nombre de symboles (chiffres) dont nous disposons pour représenter des nombres dans un système de numération détermine le type de la base. Ainsi, le système décimal est également appelé système à base 10, le système binaire système à base 2, etc.
1) Système binaire ou base 2
Binaire ou système binaire est un mode de représentation des chiffres, adapté aux composants électroniques. Ce système utilise deux chiffres 0 et 1. C'est avec ce codage que fonctionnent les ordinateurs pour coder toutes les informations. Par exemple le chiffre 19, en décimal peut être codé 10011.
2) Système octal ou base 8
Encore appelé système à base 8 ou base 8 est un moyen d'écrire les nombres avec 8 symboles soient {0, 1, 2, 3, 4, 5, 6, 7}.
Cette base permet de représenter de manière rapide et réduit les nombres exprimés en base 2. Chaque symbole à un poids. Exemple 425=4×82 + 2×81 + 5×80
Bon à savoir
Avec l'évolution technologique des composants, cette base tend aujourd'hui à disparaître au profit de la base 16. Mais toute fois elle reste encore très utilisée par certains systèmes d'exploitation comme LINUX pour accorder les droits aux fichiers, répertoires, �
3) Système hexadécimal ou base 16
Encore appelé système à base 16 est un moyen d'écrire les nombres avec 16 symboles soient {0, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}. Cette base est très utilisée en informatique pour représenter les adresses mémoires,
4) Tableau de correspondance
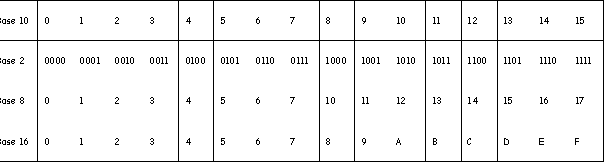
En résumé
- Un système de numération décrit la façon avec laquelle les nombres sont représentés.
- Le système de numération est caractérisé par son Alphabet (ensemble de symboles ou chiffres) et les règles d'écriture de ses nombres.
- La base est le nombre de symbole (chiffre) utilisé pour représenter les nombres dans un système de numération.
- Nous avons 4 bases usuelles : la base 10, la base 2, la base 8 et la base 16.
Conclusion
Tout ce que nous manipulons appartient à un système de numération bien défini, par exemple le français est un système de numération. Il était question pour nous de circonscrire les notions de système de numération et de base, ensuite d'énumérer les bases usuelles manipulées en informatique.
La question que nous voulons à présent résoudre est celle de savoir : Comment convertir un nombre d'une base à une autre base ? (c'est l'objet de la prochaine leçon).
A découvrir aussi
- Exercices sur la conversion d'une base à une autre base
- Conversion d’un nombre d’une base à l’autre
- Réussir l'opération d'addition dans un système de numération
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 26 autres membres
